During my exploration of the principles of databases and data management systems, I have encountered data structures that may assist in routine programming tasks. In this blog, I will elucidate my findings regarding these data structures and their applications.
Indexes
Indexes are one of the most important aspects of a database management system. They help decrease query response time by allowing the database to locate data more efficiently, without scanning the entire table. When we need to search for data based on specific columns or properties, we create an index for those attributes. There are several types of indexes, each of which is optimized for different query patterns and data characteristics.
B-tree
A generalization of the binary tree, B-trees are a type of balanced tree and frequently used as the default index type if no type is given. Its concept is simple yet effective: A B-tree of order (m) can have up to m - 1 sorted keys per node and m child pointers. The keys within each node split the key space so that all keys in a particular child node are located between two adjacent keys in the parent node. The next example explains visually how a B-tree is structured.
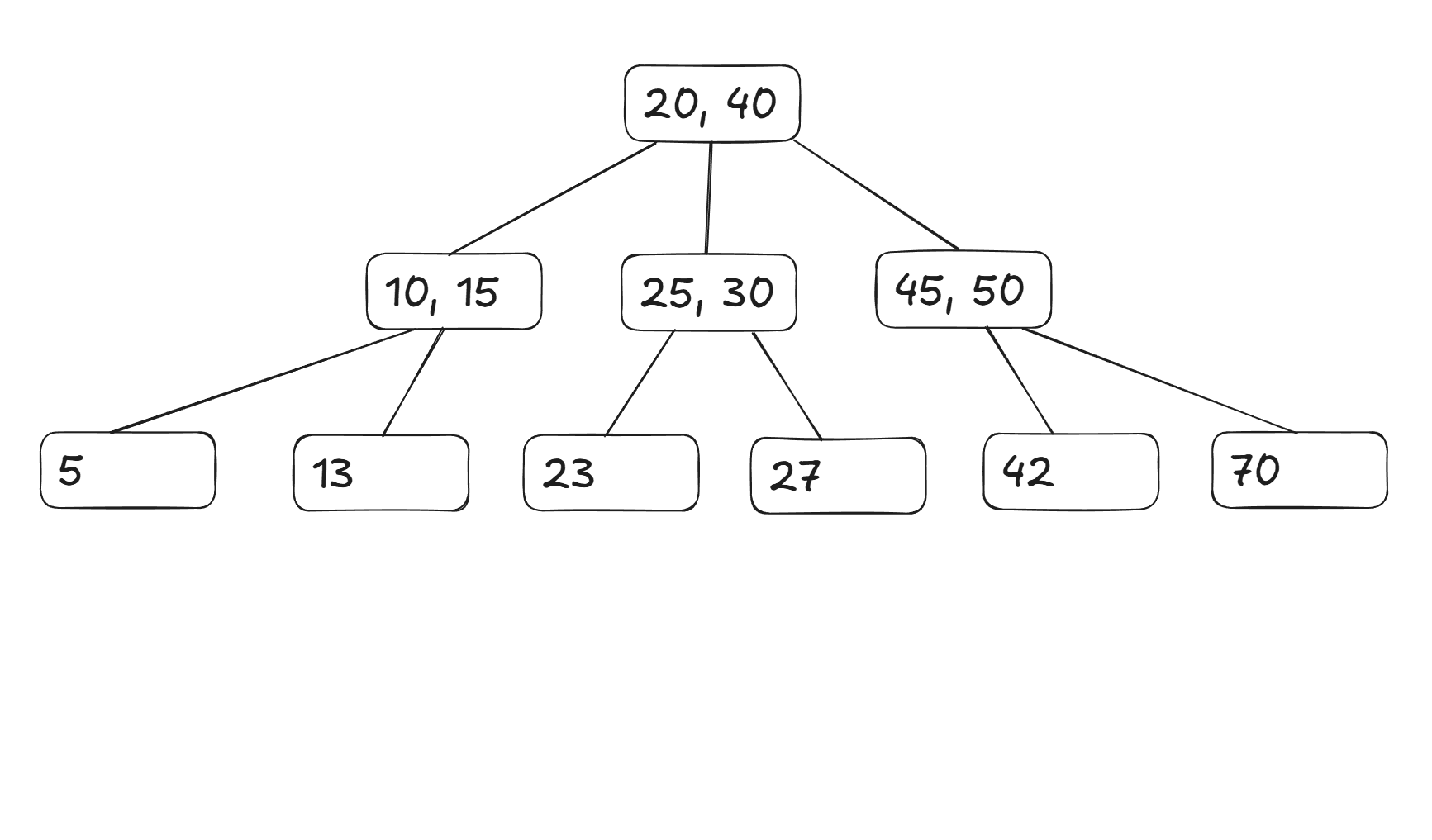
- The first child of the root contains values lower than 20.
- The second child contains values between 20 and 40.
- The third child contains values greater than 40.
If we want to locate the position of the key 27, we first go to the second child of the root (because 27 lies between 20 and 40), then descend to the second child of that node (because 27 lies between 25 and 30). Once found, all values greater than 27 can then be accessed sequentially from that point onward.
Its complexity in big O notation is always O(log n) for search, insertion, and deletion for both average and worst-case scenarios.
In practice, the majority of modern databases use a variant called a B+ tree. The difference is that a B+ tree stores all the actual data in the leaves, while the internal nodes contain only pointers for navigation. Furthermore, all leaves are sequentially connected to facilitate range queries and ordered scans.
P.S. The lower the depth of a B-tree/B+tree is, the fewer memory accesses are required to locate a record, which improves the query speed.
Hash Table
A hash table is a data structure that maps keys to values. A hash function generates a numeric value derived from the key, which serves as the index for the corresponding bucket. Each bucket stores one or more entries that hash to the same index, often implemented as a linked list (or another small container) to handle collisions.
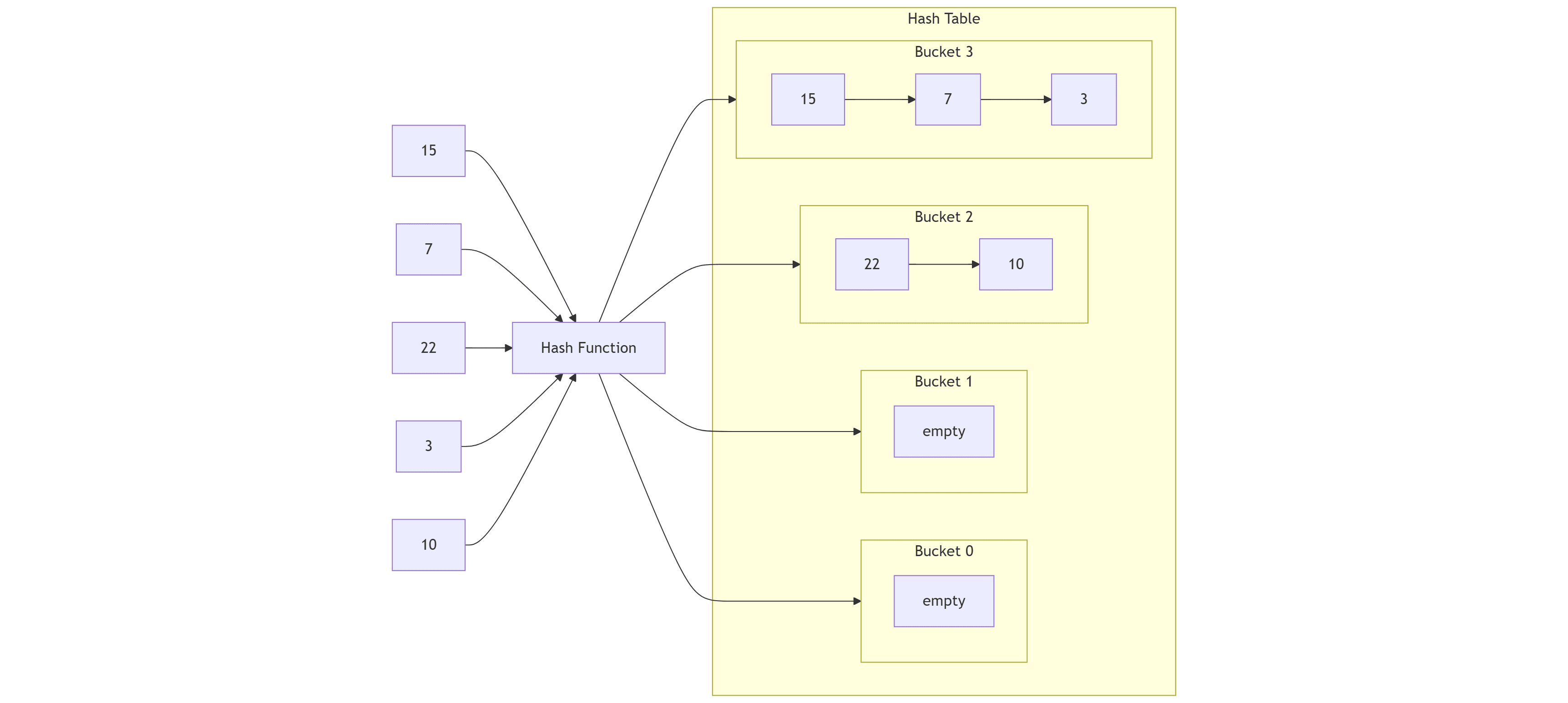
NOTE: A perfect hash table maps n keys into n buckets without collisions. In practice it is only feasible for static datasets.
Theoretically, a search cost in big-O notation is O (1+ m) (considering m the size of the bucket). Practically, databases use a good hash function and resize the hash table when the load factor α (α = n / number_of_buckets) grows too high; that keeps m very small, maintaining amortized O(1) performance.
Probabilistic data structures
Standard data structures like b-trees and linked lists are deterministic structures; they guarantee correctness but consume significant memory when dealing with large datasets. Probabilistic data structures trade a small amount of accuracy for space and speed and are used in databases, search engines, and other large-scale data systems.
Bloom filter
A bloom filter is a probabilistic data structure that tests whether an element belongs to a set or not. It depends on the number of bits in the filter (bit array) m, the number of items inserted n, and the number of hash functions k. Initially the filter is filled with zeros. To insert an element, it is passed through the k hash functions, which produce k indexes in the bit array. The bits at those positions are set to 1.
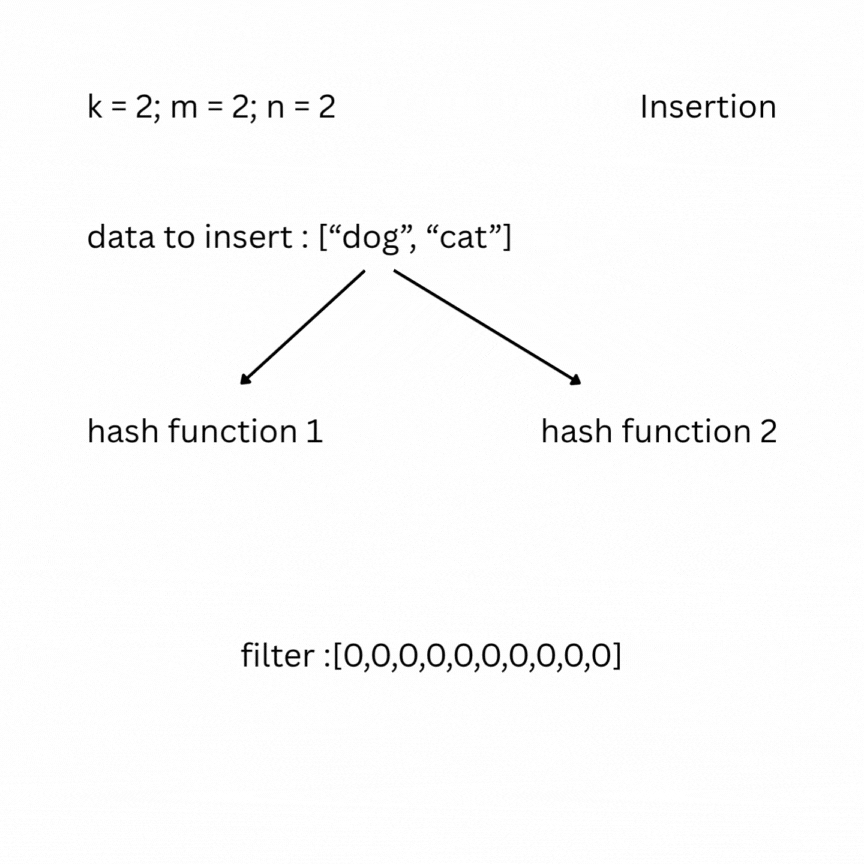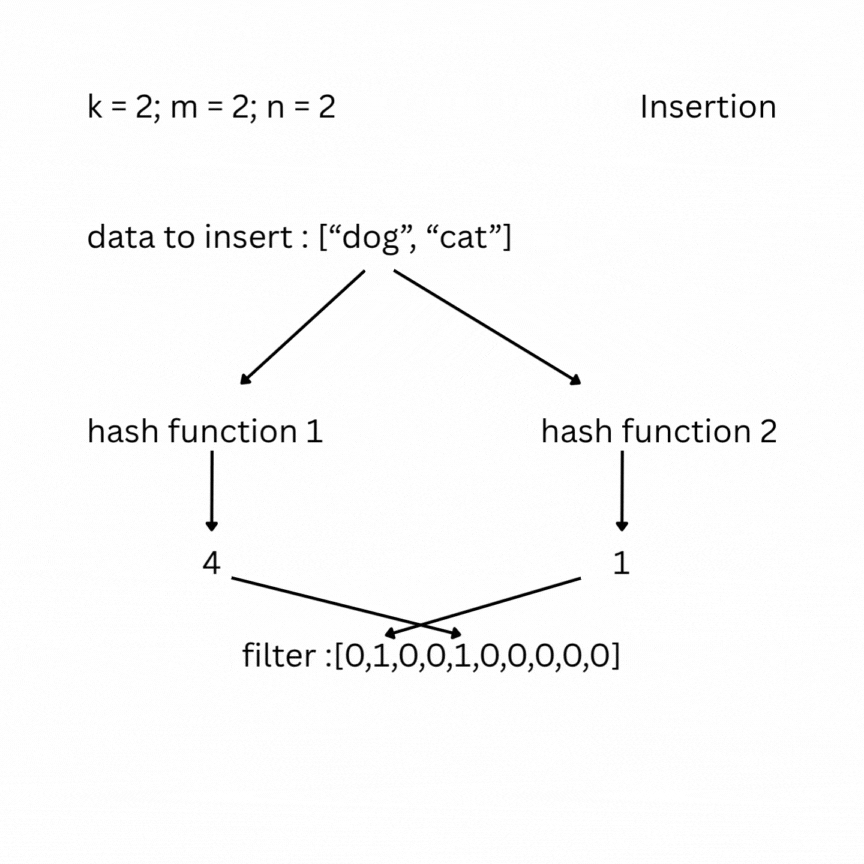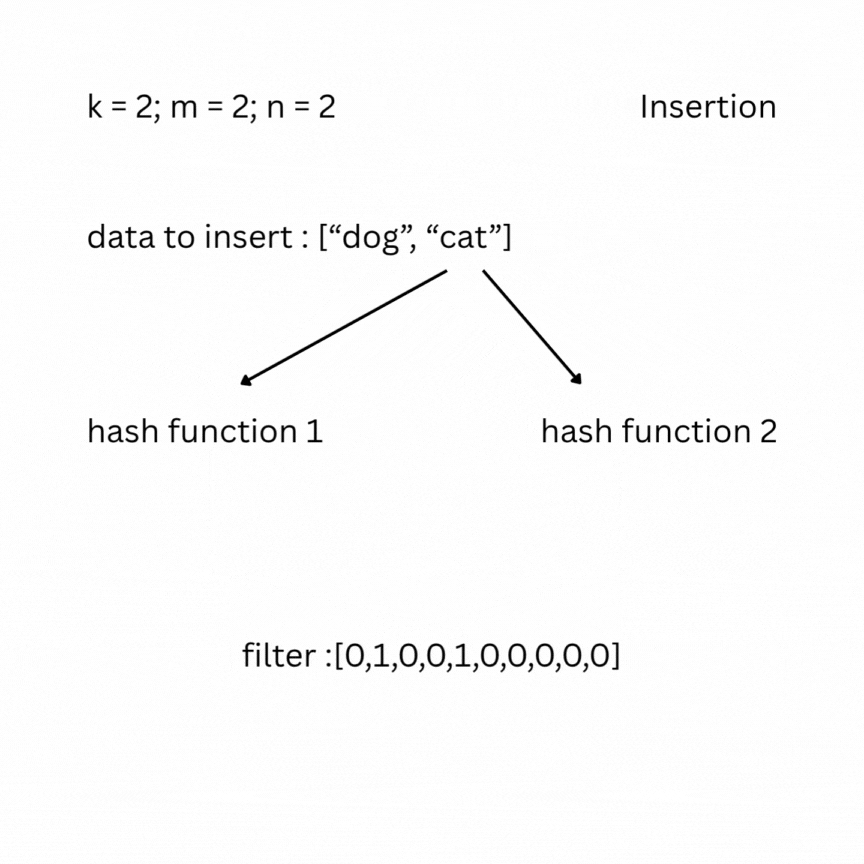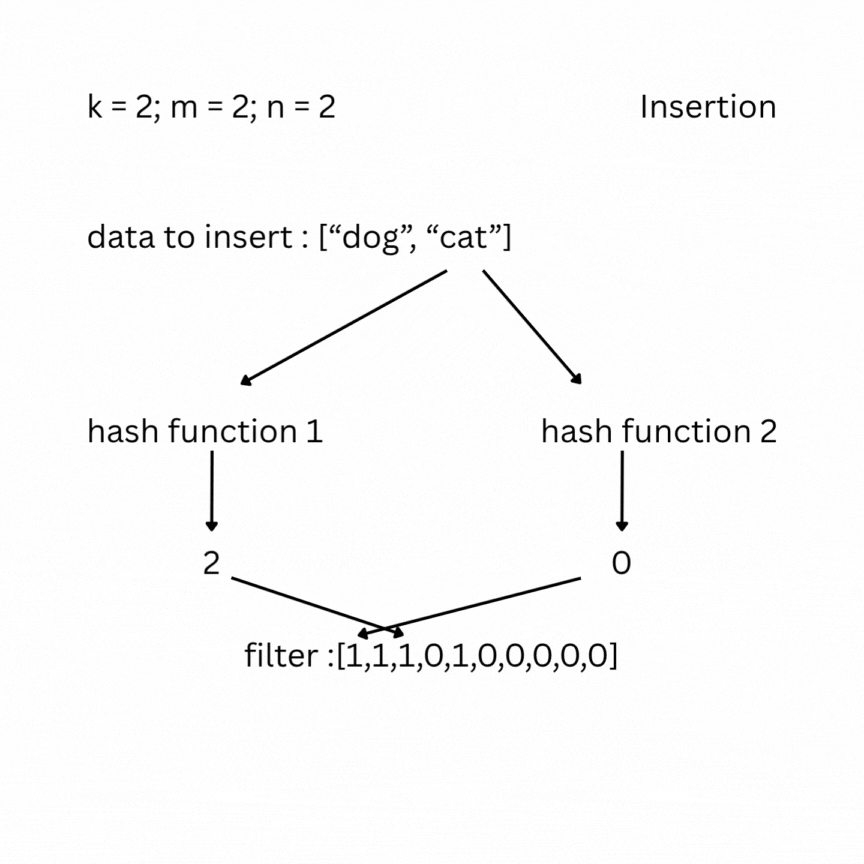
To check, you feed your entry to the hash functions and look at the indexes; if one of them has a value of 0, the data does not exist in the set; otherwise, it most likely does. False positive results are possible, but false negatives are not.
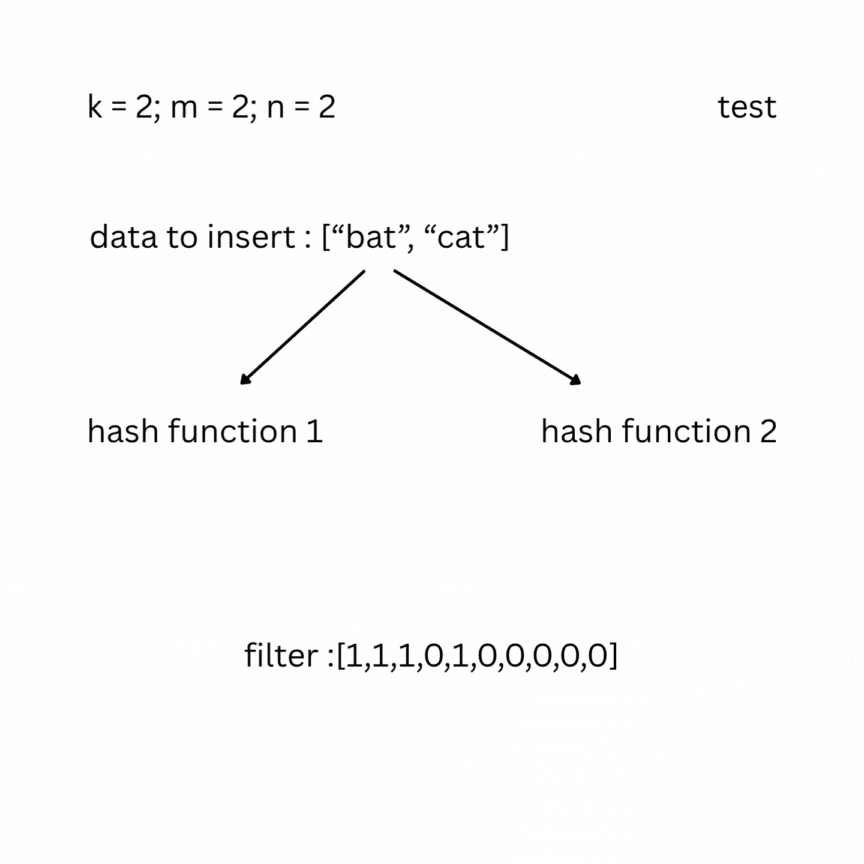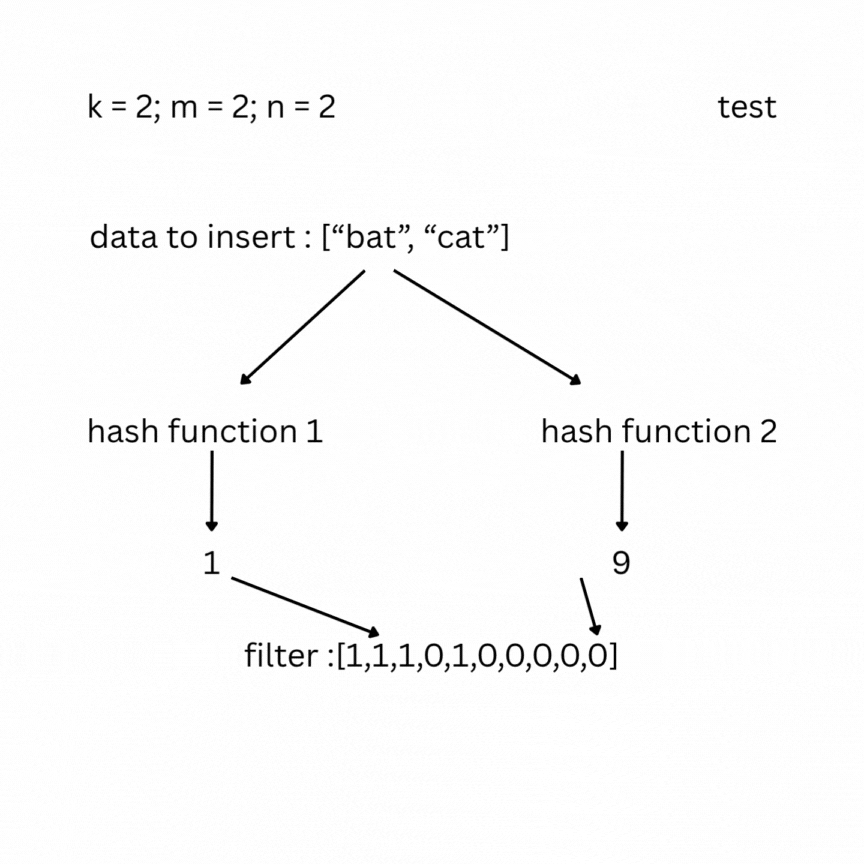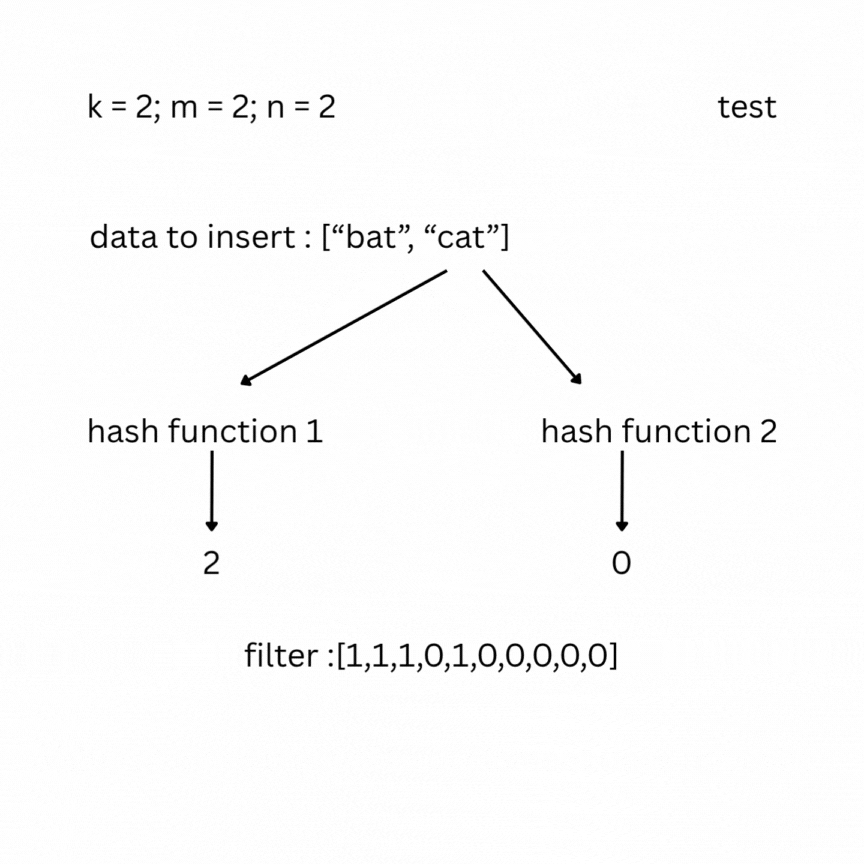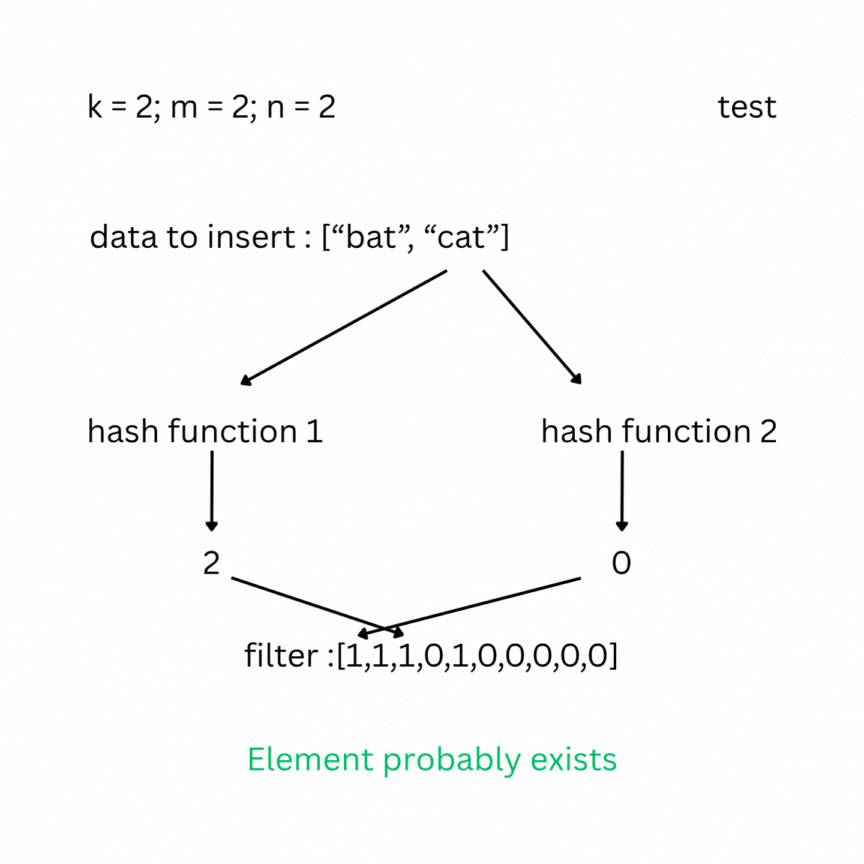
Note: As more elements are inserted, the Bloom filter becomes more saturated, and the false positive rate increases. To keep the false positive rate low, the array size m should be sufficiently large relative to n (roughly 10–15 bits per element). The optimal number of hash functions is .Under typical conditions, this keeps the false positive rate between 0.1% and 1%.
Skip list
With deterministic results and probabilistic behavior, the skip list, even though it is not the best choice for memory usage, is still a funny and reliable data structure. Its structure is interesting; there are multiple random layers of the same sorted linked list, and the higher the level, the more skipped items. Nodes with the same value are connected vertically, allowing quick movement between levels. While skip lists use more memory than arrays or B-trees, their average time complexity for search, insertion, and deletion is O(log n), making them efficient in practice.
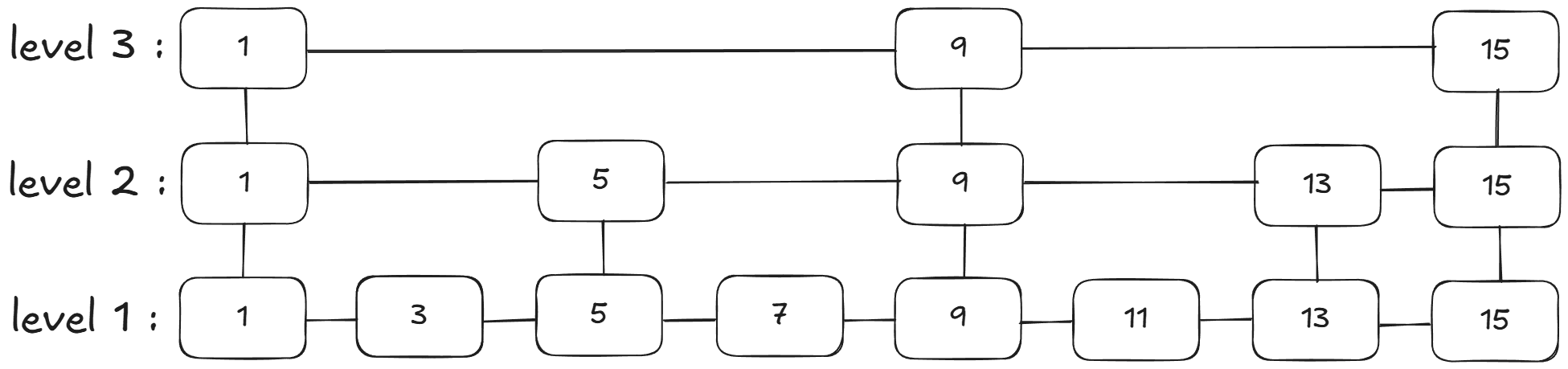
Skip lists are commonly employed in modern databases, particularly in in-memory systems and caches that demand quick, ordered access. Redis is a prime example of a system that uses skip lists to handle sorted sets (ZSET). The skip list keeps elements in score order, allowing for fast range searches, rank queries, and insertion/deletion. Skip lists are also used in key-value stores such as LevelDB and RocksDB for in-memory write buffers (memtables) prior to flushing data to disk. Their probabilistic balancing makes them easier to design than balanced trees, and they are especially well-suited to concurrent operations, in which several threads must read and write at the same time.
Note: There are many more probabilistic data structures and other types of data structures used in database indexes. The selection presented here is entirely subjective. I chose the ones that had the most impact on me.